Fibonacci partie 1
Table des matières
- Introduction
- Léonard, le mathématicien puisant dans tous les coins.
- Les lapins de Noël
- Les cases se défont quand les sections voudraient les carrés
- Des propriétés qui ne sont pas du vol
- L'aisance du cas Binet
- Le triangle de Pascal
- Somme après somme, rapport après après rapport, le nombre d'or
Intermèdes: Fibonacci hors-les-maths
- FI comme physique
- BO comme botanique
- NA comme naturels (nombres)
- CCI comme a vos souhaits !
Les sources du chapitre entier avec son Makefile Sources
1. Introduction
Ceci est un article du magazine ST magazine n° 88, rédigé pas jean pascal Duclos et adapté par timothée Ruffenach pour la version PC.
Léonard, le mathématicien puisant dans tous les coins
Il était une fois, entre 1175 et 1240, un individu répondant au nom de Fillus Bonacci (le fils de Bonaccio), que l'on prit l'habitude d'appeler Fibonacci, pas contraction, ou encore Léonard de Pise, pour le différencier sans doute de Léonard de Vinci qui devait naître deux siècles après sa mort.
Passionné dès son plus jeune âge par les mathématiques - élevé à Bougie en Algérie, il fut initié par des précepteurs musulmans - il voyagea dans tout le monde méditerranéen, et jugea que de toutes les méthodes de calcul, les méthodes hindoues étaient les meilleurs.
Il fit le point dans son ouvrage Liber abacci (le livre des abaques, 1202) des connaissances dues à Euclide.
Dans cet ouvrage et d'autre il expose les connaissances mathématiques des arabes, donne des rudiments de trigonométrie, et calcul le nombre pi avec six décimales, dont quatre correctes. On lui doit surtout l'introduction des chiffres arabes dans l'introduction des chiffres arabes dans la numération - ce qui eut peu d'influence sur les commerçants de l'époque, habitués au chiffres romains - et les bases du symbolisme dans l'écriture mathématique, que complétera François Viète au seizième siècle.
Tout cela pour dire que Léonard n'était pas le premier venu, et qu'il serait hâtif de la considérer simplement comme un compteur de lapins.
Malgré son apport aux mathématiques, Léonard serait tombé dans l'oubli sans un arithméticien français du XIX siècle, Édouard Lucas, qui proposera l'étude des lapins de Fibonacci, le lapin de Fibonacci devenant alors aussi célèbre que le mouton de Panurge, l'âne de Buridan ou la mule du pape.
Les lapins de Noël
De quoi s'agit-il ? Fibonacci imagine que l'on dispose d'un couple de lapins. Ceux-ci, comme on sait, se reproduisent... comme des lapins.
Pour simplifier, chaque couple de lapins engendre un nouveau couple de lapins dès la deuxième génération, puis procrée un couple par génération.
Pour simplifier, chaque génération a une durée d'un mois.
Chaque couple nouveau subit la même loi. La mort, la maladie ou toute autre raison ne sauraient entraver l'inéluctable loi (il s'agit hélas d'une vue de l'esprit... mais Fibonacci n'étudiait que le nombre de lapins en un an, soit douze générations).
Combien de lapins vivront à la N-ième génération ?
Pour répondre à cette fondamentale question, on peut s'aider d'un diagrame:
génération 0: 1 couple de lapins tout neuf : A
génération 1: 1 couple de lapins (le même)
génération 2: 2 couples: A et B engendré par A
génération 3: 3 couples: A, B, et C engendré par A
génération 4: 5 couples: A, B, C, D (par A), E(par B)
génération 5: 8 couples: A, B, C, D, E, F(par A), G(par B), H(par C)
...etc. La suite des nombres obtenus vérifie, à partir du rang 2, la relation u(n) = u(n-1) + u(n-2) où chaque terme est égal à la suite des deux termes précédent.
Je vous donne les codes sources en C d'un programme qui calcul le u(n) Source de fibonacci
C'est à dire la suite dont les premiers termes sont : 1, 1, 2, 3, 5, 8, 13, 21 34, 55, 89, 144, 233, 377, 610,...
Voici une courbe sur 18 génération qui montres que cette suite croit de manière exposentiel.
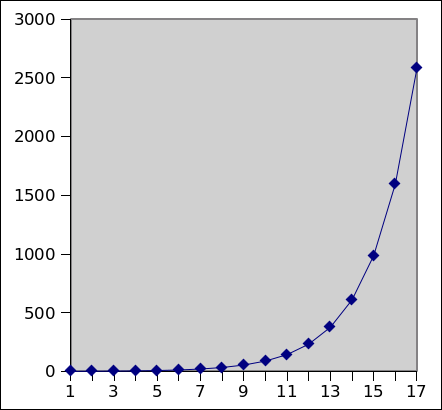
C'est une suite évidemment croissante, qui possède un grand nombre de propriétés diverses: par exemple, si u, v et w sont trois termes consécutifs de cette suite, le produit de uw et le carré v² ont toujours une différence de 1 ou -1, alternativement.
Exemple : u=2, v=3, w=5 uw = 2*5 = 10 v² = 3*3 = 9 donc 10-9 = 1 donc il y a une différence 1.
Si on prend la suite suivante ça donne u=3, v=5, w=8 uw = 3*8 = 24 v² = 25 donc 24-25 donc il y a une différence de -1 ce qui prouve que la différence alterne toujours de 1 ou -1.
En fait, on peut démontrer la relation u(n)*(u(n+2) = (u(n+1))² + (-1)^n, pour simplifier on peut dire par rapport à si dessus u(n) = u, u(n+2) = w, (u(n+1)² = v et que (-1)^n est l'alternance 1 ou -1.
Je vous donne les codes sources en C d'un programme qui vérifie bien la suite de trois termes consécutifs de fibonacci Source de suite
Afin de ne pas trop mathiser le lecteur (NDLR: s'il ne l'est pas avec ça...). disons simplement que la démonstration utilise la récurence, et que la relation est connue sous le nom de relation de Simson (celui de la droite).
Les cases se défont quand les sections voudraient les carrés
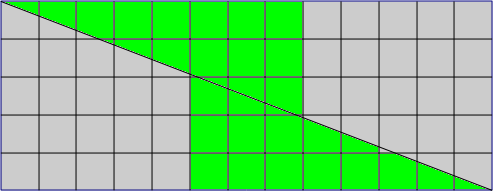
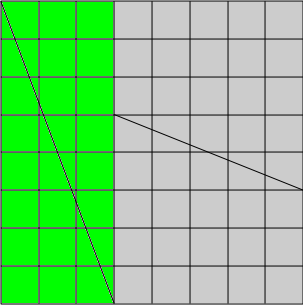
Cette propriété permet la réalisation d'un "paradoxe" étonnant: on trace sur du carton quadrillé un rectangle dont les côtés sont deux nombres de Fibronacci.
On peut découper ce rectangle en quatre morceaux afin de reformer un carré.
On constate alors que l'une des cases a disparu, ou que au contraire, une case supplémentaire apparaît, par exemple, un rectangle de 5 cases sur 13 - 65 cases - donne après découpage un carré de 8 cases de côté - 64 cases.
Il paraît que lewis Carroll était très friand de ce tour de passe-passe, nul doute que le Lapin blanc d'Alice ne soit un lapin de Fibonacci !.
Des propriété qui ne sont pas du vol
On peut remarquer aussi que la somme des n premiers terme est égale au terme de rang n+2 moins 1:
1 = 2 - 1
1 + 1 = 3 - 1
1 + 1 + 2 = 5 - 1
1 + 1 + 2 + ...... + 144 = 377 - 1
Voici les sources d'un programme qui vérifie cette méthode Source de rangMoins1
Ou encore u(n) est un diviseur de u(2n+1):
1 divise 1
1 divise 3
2 divise 8
13 divise 377
etc...
Voici les sources d'un programme qui vérifie cette méthode Source de divise
Quelques autres propriétés:
1 + 2 = 3
1 + 2 + 5 = 8
1 + 2 + 5 + 13 = 21
u(0) + u(2) + ... + u(2n) = u(2n+1)
Voici les sources d'un programme qui vérifie cette méthode Source de suite2
1 + 3 = 5 - 1
1 + 3 + 8 = 13 - 1
1 + 3 + 8 + 21 = 34 - 1
u(1) + u(3) + ... + u(2n -1) = u(2n) - 1
Voici les sources d'un programme qui vérifie cette méthode Source de suite3
1 - 1 + 2 = 1 + 1
1 - 1 + 2 - 3 = - 2 + 1
1 - 1 + 2 - 3 + 5 = 3 + 1
1 - 1 + 2 - 3 + 5 - 8 = - 5 + 1
1 - 1 + 2 - 3 + 5 - 13 = 8 + 1
Voici les sources d'un programme qui vérifie cette méthode Source de suite4
2² - 1² = 3
3² - 1² = 8
5² - 2² = 21
8² - 3² = 55
13² - 5² = 144
u(n)² - u(n-2)² = u(2n-1)
Voici les sources d'un programme qui vérifie cette méthode Source de suite5
Et, pour finir en beauté:
1² = 1 * 1
1² + 1² = 1 * 2
1² + 1² + 2² = 2 * 3
1² + 1² + 2² + 3² + 5² + 8² = 8 * 13
soit 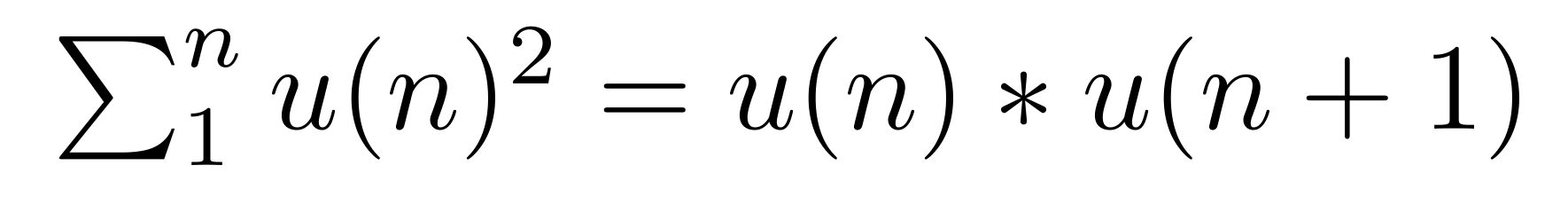
Voici les sources d'un programme qui vérifie cette méthode Source de suite5
L'aisance du cas Binet
Toutes ces propriétés et bien d'autres, que je laisse au lecteur le soin de découvrir, se vérifient aisément jusqu'aux rangs les plus élevés à l'aide de l'ordinateur.
Il suffit de savoir calculer le terme de Fibonacci de rang n.
Pour calculer le nombre de Fibonacci de rang n, on peut calculer par incrémentation successive, ou mieux en utilisant la récursivité par auto-appel d'une procédure.
On peut aussi utiliser la formule de Binet (pas l'auteur des Bidonchon, l'autre) pour calculer aisément les nombres de Fibonacci:
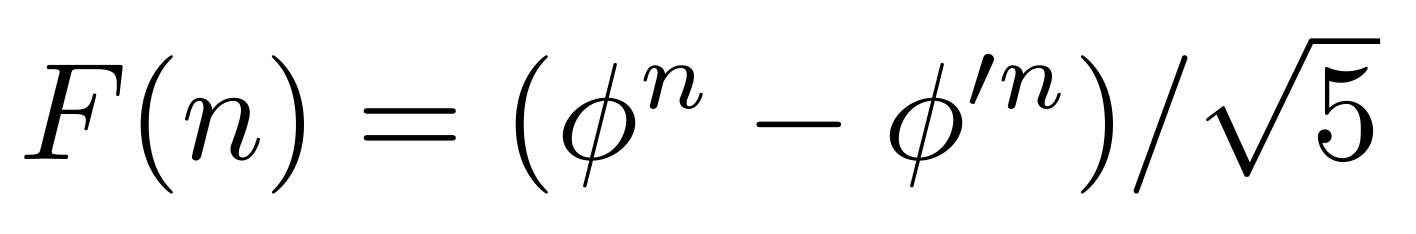
où Φ représente le nombre d'or (voir ci dessous), Φ' le conjugué du nombre d'or, c'est-à-dire les nombres:

F(n) peut être calculé comme l'entier le plus proche de :
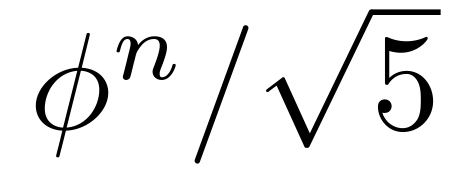
Remarquons que ces deux formules donnent le terme F(n) d'une suite vérifient F(0) = 0, F(1) = 1, F(2) = 1, etc... c'est-à-dire que l'on a u(n) = F(n+1).
Il faut y penser pour vérifier les propriétés proposées au chapitre précédent.
Voici les sources qui permettent de calculer la suite de Fibonacci avec la méthode Binet Source de binet
Le triangle de Pascal
Parmi mes curiosités mathématique liées aux nombres de Fibonacci, l'une se rattache au fameux triangle de Pascale (Blaise, celui qui écrit quand il pense), que tout matheuphile paresseux connaît, puisqu'il permet de calculer les coefficients de la décomposition de (a+b)^n sans autres calculs qu'une série d'additions.
Additions dont le PC se chargera bien volontiers !
Rappelons que chaque terme du triangle est la somme des deux situés au dessus de lui :
1
1____1
1____2____1
1____3____3____1
1____4____6____4____1
1____5___10___10____5____1
1____6___15___20___15____6____1
Voici les sources qui affiche le triangle de pascal Source de pascal
On sait que la somme des termes d'une même ligne donne toujours 2^n: 1 = 2^0, 1 + 1 = 2^1, 1 + 2 + 1 = 2^2, 1 + 3 + 3 + 1 = 2^3, etc..
Si on effectue les sommes des termes selon les diagonales, on trouvera :
1 = 1
1 = 1
1 + 1 = 2
1 + 2 = 3
1 + 3 + 1 = 5
1 + 4 + 3 = 8
1 + 5 + 6 + 1 = 13
Vous aurez reconnu la suite de notre Léonard, sinon c'est à désespérer !
Or chacun des termes du triangle de Pascal est le nombre C(n,p): combinaison de n objets p à p, défini par: c(n, p) = n! / p!(n-p)! (n! signifie n(n-1)(n-2)...2.1), je vous laisse imaginer la belle formule que l'on peut écrire !.
Notons pour conclure ces propriétés (que les maths adorent) que les récents développements de l'informatique ont relancé l'intérêt pour ces suites parce qu'elles sont des applications pratiques dans le classement des données, la recherche des informations, la génération de nombre aléatoires, et certaines méthode rapides d'approximation des extrema de fonction compliquées dons les dérivées sont inconnues.
Pour briller en société (?), sachez enfin que la suite de Fibonacci intervient dans la démonstration du dixième de Hilbert (Vous savez le type aux sysygies ...)!
somme après somme, rapport après rapport, le nombre d'or
La propriété la plus connue de la suite de Fibonacci reste quand même celle concernant le rapport de deux termes consécutifs: quand n tend vers l'infini, le rapport: v(n) = F(n+1)/F(n) tend vers une limite, et cette limite est le nombre d'or.
Le nombre d'or, celui des mathématiciens et non celui des astronomes, est tout simplement la racine positive de l'équation: x²-x-1=0
Le calcul de Delta Egalbé de Moinquatrasset (vielle noblesse au second degré) nous donne les valeurs déjà citées Φ et Φ':

Mais pourquoi poser cette équation ? Au départ, pour établir une règle d'esthétique: partager l'unité en deux parties a et b afin que leur rapport a/b=x soit le même que le rapport de la plus grande au tout 1/a.
Or a + b = 1. donc:
(a + b)/a = x
1 + (b/a) = x
1 + (1/x) = x
et, en multipliant par x:
x + 1 = x²
Ce nombre d'or joue un rôle considérable tant dans l'analyse de phénomènes naturels que dans des branches très diverses des mathématiques, de la physique, de la biologie, et même dans des domaines où on ne s'attendrait pas à le trouver. Nous aurons l'occasion d'en reparler dans une prochaine rubrique... ou plusieurs, tant le sujet est vaste. Mais revenons au sujet du mois, les nombre de Fibonacci.
FI comme Physique
On donne le circuit électrique donné par le schéma ci dessous, où Ze désigne l'impédance d'entrée, Zs l'impédance de sortie, et An le rapport entre la différence de potentiel aux bornes de la sortie.

On a les valeurs suivantes:
n______: 1___2___3
Ze en Ω_: 2___5/3_13/8
Zs en Ω_: 1___2/3_5/8
An_____: 2___5___13
On établit par récurence:
Ze = F(2n + 1) / F(2n)
Zs = F(2n - 1) / F(2n)
An = F(2n + 1)
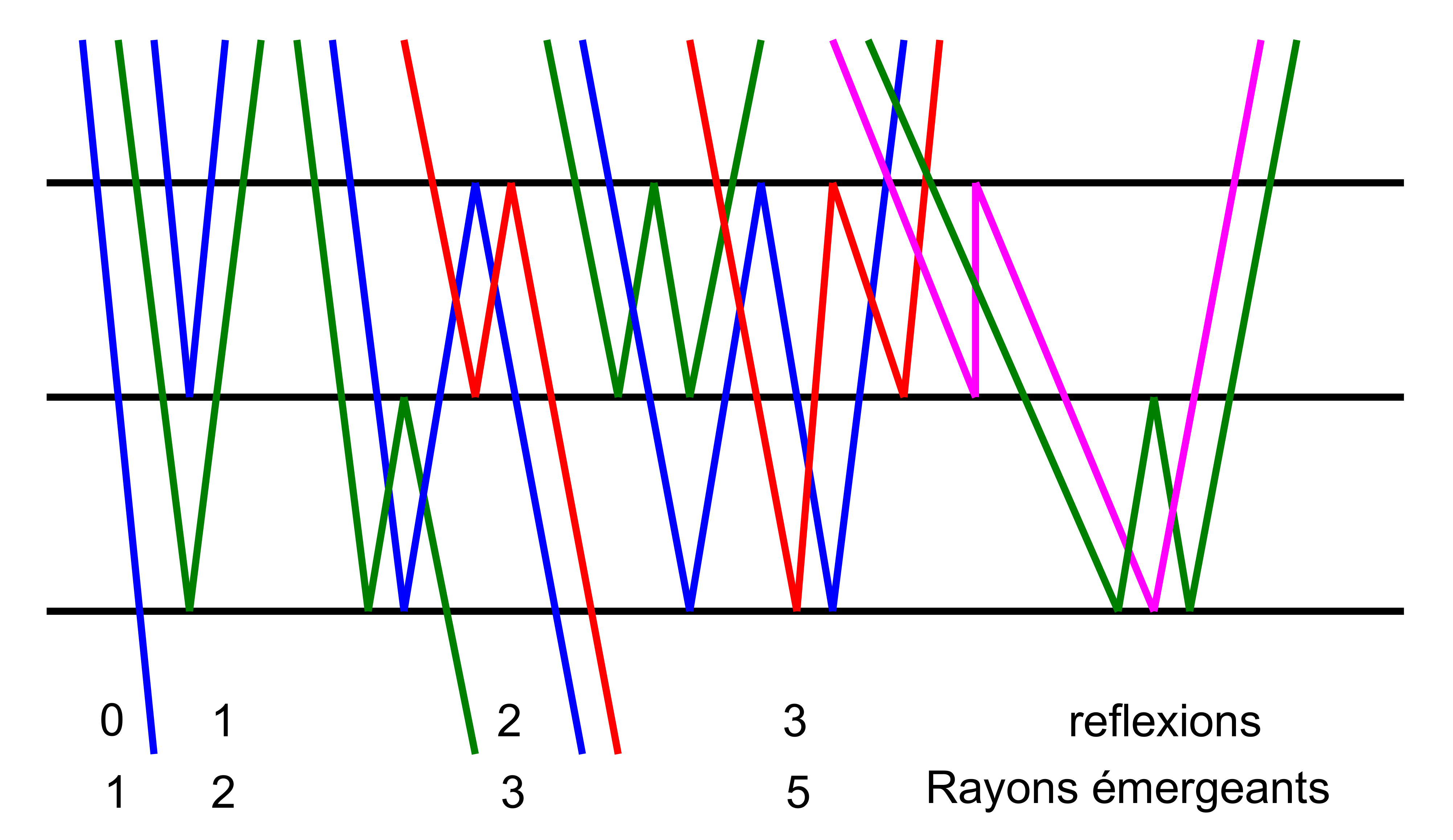
En optique.
Le nombre de rayons lumineux émergeant après un certain nombre de lames de verre à face parallèles est un nombre de Fibonacci.
BO comme botanique
Les branches, feuilles, fleurs ou graines sont assemblés et arrangées selon un certain motif général.
On y trouve souvent des nombres de Fibonacci:
Nombre de pétales des fleurs courantes:
La circée a deux pétales
L'iris, le lis, la tulipe ont trois pétales
Le bouton d'or,le delphinium, l'anémone, etc, ont cinq pétales
Delphinium, anémone, ficaire en ont huit (selon espèces)
Jacobée, camomille, marguerite en ont treize
Aster, chicorée, doronique: 21 pétales
Paquerette, marguerite des champs, plantain: 34 pétales
Aster d'automne: 55 ou 89 pétales
Ce motif n'est pas nécessairement suivi par toutes les plantes d'une même espèce, mais semble être une caractéristique de l'espèce.
Si des trèfles à quatre feuilles existent, ils sont pourtant moins nombreux que ceux dont le nombre de feuilles est F(4).
Position des feuilles le long d'une tige:
Les feuilles poussent régulièrement autour de la tige en décrivant des hélices.
En général, le nombre de feuilles nf entre deux feuilles placées directement l'une au dessus l'autre et le nombre de révolutions nr entre ces deux même feuilles sont des nombre de Fibonacci.
La mesure en nombre de tours de l'angle entre deux feuille est alors nf / nr.
Ainsi pour le tilleul et l'orme ce rapport est de 1/2, pour le hêtre et le noisetier 1/3, pour le chêne, l'abricotier, le cerisier 2/5, pour le peuplier et le poirier 3/8, pour le saule et l'amandier 5/13.
Le même angles est conservé pour une même espèce dans la disposition des branches, des fleurs et des bourgeons.
On constate en outre que les rapports les plus courants, 1/2, 1/3, 2/5, 3/8, 5/12, 8/21, ... sont de la forme F(n-2)/F(n), ce qui correspond à un nombre de tours voisin de 1/Φ².
Or, on démontre que pour toutes les feuilles, l'angle entre deux feuilles doit mesurer 1/Φ², (ou 1 / Φ selon l'orientation choisie, puisque 1/Φ² + 1/Φ = 1).
Spirales
Le coeur d'une fleur de tournesol ou de marguerite présente des graines réparties en spirales, l'une dans un sens, l'autre dans l'autre.
Le nombre de spirales dans chaque sens sont fréquemment des nombres de Fibonacci: 21 et 34, 34 et 55 ou 55 et 89 pour les fleurs de tournesol, 21 et 34 pour les marguerites.
On remarque le même phénomène pour les pommes de pin (3 et 5 ou 5 et 8 spirales) et pour les ananas (trois familles de spirales, puisque la structure n'est plus plane, de 5, 8 et 13 spirales.
Toutes ces règles souffrent des exceptions, mais apparaissent comme une tendance générale.
NA comme naturels (nombres)
Tout nombre entier se décompose en une somme de nombres de Fibonacci distincts.
De plus la décomposition est unique si l'on s'interdit deux nombres de Fibonacci consécutifs et si l'on prend les nombres de Fibonacci à partir de F(2), puisque 1 figure deux fois.
Cette propriété, qui porte le joli nom de théorème de Zeckendorf, nous replonge dans les maths.
Laissons de côté la démonstration - qui utilise la récurence - et bornons-nous à donner quelques résultats:
1 = 1
2 = 2
3 = 3
4 = 3 + 1
5 = 5
6 = 5 + 1
...................
25 = 21 + 3 + 1
46 = 34 + 8 + 3 + 1
88 = 55 + 21 + 8 + 3 + 1
Voici les sources qui calculent les suites ci-dessus Source de naturels
On peut s'intéresser au nombre d'éléments dans la décomposition de Fibonacci d'un nombre.
Ainsi, n(5) = 1, n(6) = 2, n(25)= 3, n(88) = 5, n(89) = 1, etc...
On obtient une loi récursive du plus bel effet.
Divisibilité: F(nk) est divisible par F(n) pour tout n et pour tout k.
Ça alors! Par exemple, F(5) = 5, F(10) = 55, F(15) = 610, F(20) = 6765: F(5) divise tous les autres, F(10) divise F(20).
Pour tout entier naturel n, il existe au moins un nombre de Fibonacci divisible par n parmi les n² - 1 premiers.
Par exemple, 6 divise F(12) et 12 < 36 ; 7 divise F(8) et 8 < 49.
Existe-t-il un nombre n qui divise seulement F(n²-1)?
A vos claviers!.
Voici les sources qui calculent les testes de divisibilités Source de divisible
C'est presque de la magie des nombres: Si F(n) est pair, alors n est divisible par 3, n est divisible par 4
Si F(n) est divisible par 5, n est divisible par 5
Si F(n) est divisible par 11, n est divisible par 10
Existe-t-il d'autres propriétés semblables ?
La réciproque de chacune est-elle vrai ?
A vos clef usb!
CCI comme a vos souhaits !
Vous n'êtes pas obligé de me croire, mais si on ne conserve que le chiffre des unités des nombres de Fibonacci, c'est-à-dire la suite a(n) = F(n) MOD 10, on obtient une série de 60 nombres qui se répète indéfiniment - une période, en quelque sorte.
Plus curieux, ce résultat est vrai pour toute suite de la forme a(n) = F(n) MOD k, où, k est un entier quelconque, la longueur de la période pouvant varier.
Exemples:
k = 2 Période 3: 0 1 1
k = 3 Période 8: 0 1 1 2 0 2 2 1
k = 4 Période 6: 0 1 1 2 3 1
k = 5 Période 20.................... à vous de jouer !
Je vous recommande particulièrement k = 30 (période 120), k = 98 (période 336), k = 125 (période 500).
Voici les sources qui calculent a(n) = F(n) MOD 60 Source de 60
Voici les sources qui calculent a(n) = F(n) MOD k Source de periode
On pourrait discourir encore longtemps sur les tours et détours de Léonard de Pise et de ses nombres, dont l'inventeur n'avait sous doute pas mesuré l'étendue des propriétés.
Ajoutons que Lucas - le "découvreur" à également laissé son nom à une suite similaire, définie de la même façon mais dont les premiers nombres sont 1 et 3.
Le propriétés des nombres de Lucas sont aussi nombreuses que celles des nombres de Fibonacci, qu'elle recoupent souvent.
Nous en reparlerons prochainement, et parlerons plus longuement du nombre d'or dont il ne faudrait pas faire phi (pardon fi)!
Un grand merci à MM Meyer et Steyaert pour leur remarquable documentation, à André Déledicq mon respectueux hommage, ainsi qu'à toute l'équipe de l'IREM de Paris VII, à Martin Gardner l'assurance de ma lucidité, et à tous les lecteurs et lectrices de ST Mage, salut !
Jean Pascal Duclos
Revenir au haut de la page
Ceci est un article du magazine ST magazine n° 88, rédigé pas jean pascal Duclos et adapté par timothée Ruffenach pour la version PC.
Léonard, le mathématicien puisant dans tous les coins
Il était une fois, entre 1175 et 1240, un individu répondant au nom de Fillus Bonacci (le fils de Bonaccio), que l'on prit l'habitude d'appeler Fibonacci, pas contraction, ou encore Léonard de Pise, pour le différencier sans doute de Léonard de Vinci qui devait naître deux siècles après sa mort.
Passionné dès son plus jeune âge par les mathématiques - élevé à Bougie en Algérie, il fut initié par des précepteurs musulmans - il voyagea dans tout le monde méditerranéen, et jugea que de toutes les méthodes de calcul, les méthodes hindoues étaient les meilleurs.
Il fit le point dans son ouvrage Liber abacci (le livre des abaques, 1202) des connaissances dues à Euclide.
Dans cet ouvrage et d'autre il expose les connaissances mathématiques des arabes, donne des rudiments de trigonométrie, et calcul le nombre pi avec six décimales, dont quatre correctes. On lui doit surtout l'introduction des chiffres arabes dans l'introduction des chiffres arabes dans la numération - ce qui eut peu d'influence sur les commerçants de l'époque, habitués au chiffres romains - et les bases du symbolisme dans l'écriture mathématique, que complétera François Viète au seizième siècle.
Tout cela pour dire que Léonard n'était pas le premier venu, et qu'il serait hâtif de la considérer simplement comme un compteur de lapins.
Malgré son apport aux mathématiques, Léonard serait tombé dans l'oubli sans un arithméticien français du XIX siècle, Édouard Lucas, qui proposera l'étude des lapins de Fibonacci, le lapin de Fibonacci devenant alors aussi célèbre que le mouton de Panurge, l'âne de Buridan ou la mule du pape.
Les lapins de Noël
De quoi s'agit-il ? Fibonacci imagine que l'on dispose d'un couple de lapins. Ceux-ci, comme on sait, se reproduisent... comme des lapins.
Pour simplifier, chaque couple de lapins engendre un nouveau couple de lapins dès la deuxième génération, puis procrée un couple par génération.
Pour simplifier, chaque génération a une durée d'un mois.
Chaque couple nouveau subit la même loi. La mort, la maladie ou toute autre raison ne sauraient entraver l'inéluctable loi (il s'agit hélas d'une vue de l'esprit... mais Fibonacci n'étudiait que le nombre de lapins en un an, soit douze générations).
Combien de lapins vivront à la N-ième génération ?
Pour répondre à cette fondamentale question, on peut s'aider d'un diagrame:
génération 0: 1 couple de lapins tout neuf : A
génération 1: 1 couple de lapins (le même)
génération 2: 2 couples: A et B engendré par A
génération 3: 3 couples: A, B, et C engendré par A
génération 4: 5 couples: A, B, C, D (par A), E(par B)
génération 5: 8 couples: A, B, C, D, E, F(par A), G(par B), H(par C)
...etc. La suite des nombres obtenus vérifie, à partir du rang 2, la relation u(n) = u(n-1) + u(n-2) où chaque terme est égal à la suite des deux termes précédent.
Je vous donne les codes sources en C d'un programme qui calcul le u(n) Source de fibonacci
C'est à dire la suite dont les premiers termes sont : 1, 1, 2, 3, 5, 8, 13, 21 34, 55, 89, 144, 233, 377, 610,...
Voici une courbe sur 18 génération qui montres que cette suite croit de manière exposentiel.

C'est une suite évidemment croissante, qui possède un grand nombre de propriétés diverses: par exemple, si u, v et w sont trois termes consécutifs de cette suite, le produit de uw et le carré v² ont toujours une différence de 1 ou -1, alternativement.
Exemple : u=2, v=3, w=5 uw = 2*5 = 10 v² = 3*3 = 9 donc 10-9 = 1 donc il y a une différence 1.
Si on prend la suite suivante ça donne u=3, v=5, w=8 uw = 3*8 = 24 v² = 25 donc 24-25 donc il y a une différence de -1 ce qui prouve que la différence alterne toujours de 1 ou -1.
En fait, on peut démontrer la relation u(n)*(u(n+2) = (u(n+1))² + (-1)^n, pour simplifier on peut dire par rapport à si dessus u(n) = u, u(n+2) = w, (u(n+1)² = v et que (-1)^n est l'alternance 1 ou -1.
Je vous donne les codes sources en C d'un programme qui vérifie bien la suite de trois termes consécutifs de fibonacci Source de suite
Afin de ne pas trop mathiser le lecteur (NDLR: s'il ne l'est pas avec ça...). disons simplement que la démonstration utilise la récurence, et que la relation est connue sous le nom de relation de Simson (celui de la droite).
Les cases se défont quand les sections voudraient les carrés
Cette propriété permet la réalisation d'un "paradoxe" étonnant: on trace sur du carton quadrillé un rectangle dont les côtés sont deux nombres de Fibronacci.
On peut découper ce rectangle en quatre morceaux afin de reformer un carré.
On constate alors que l'une des cases a disparu, ou que au contraire, une case supplémentaire apparaît, par exemple, un rectangle de 5 cases sur 13 - 65 cases - donne après découpage un carré de 8 cases de côté - 64 cases.
Il paraît que lewis Carroll était très friand de ce tour de passe-passe, nul doute que le Lapin blanc d'Alice ne soit un lapin de Fibonacci !.


Des propriété qui ne sont pas du vol
On peut remarquer aussi que la somme des n premiers terme est égale au terme de rang n+2 moins 1:
1 = 2 - 1
1 + 1 = 3 - 1
1 + 1 + 2 = 5 - 1
1 + 1 + 2 + ...... + 144 = 377 - 1
Voici les sources d'un programme qui vérifie cette méthode Source de rangMoins1
Ou encore u(n) est un diviseur de u(2n+1):
1 divise 1
1 divise 3
2 divise 8
13 divise 377
etc...
Voici les sources d'un programme qui vérifie cette méthode Source de divise
Quelques autres propriétés:
1 + 2 = 3
1 + 2 + 5 = 8
1 + 2 + 5 + 13 = 21
u(0) + u(2) + ... + u(2n) = u(2n+1)
Voici les sources d'un programme qui vérifie cette méthode Source de suite2
1 + 3 = 5 - 1
1 + 3 + 8 = 13 - 1
1 + 3 + 8 + 21 = 34 - 1
u(1) + u(3) + ... + u(2n -1) = u(2n) - 1
Voici les sources d'un programme qui vérifie cette méthode Source de suite3
1 - 1 + 2 = 1 + 1
1 - 1 + 2 - 3 = - 2 + 1
1 - 1 + 2 - 3 + 5 = 3 + 1
1 - 1 + 2 - 3 + 5 - 8 = - 5 + 1
1 - 1 + 2 - 3 + 5 - 13 = 8 + 1
Voici les sources d'un programme qui vérifie cette méthode Source de suite4
2² - 1² = 3
3² - 1² = 8
5² - 2² = 21
8² - 3² = 55
13² - 5² = 144
u(n)² - u(n-2)² = u(2n-1)
Voici les sources d'un programme qui vérifie cette méthode Source de suite5
Et, pour finir en beauté:
1² = 1 * 1
1² + 1² = 1 * 2
1² + 1² + 2² = 2 * 3
1² + 1² + 2² + 3² + 5² + 8² = 8 * 13
soit ![]()
Voici les sources d'un programme qui vérifie cette méthode Source de suite5
L'aisance du cas Binet
Toutes ces propriétés et bien d'autres, que je laisse au lecteur le soin de découvrir, se vérifient aisément jusqu'aux rangs les plus élevés à l'aide de l'ordinateur.
Il suffit de savoir calculer le terme de Fibonacci de rang n.
Pour calculer le nombre de Fibonacci de rang n, on peut calculer par incrémentation successive, ou mieux en utilisant la récursivité par auto-appel d'une procédure.
On peut aussi utiliser la formule de Binet (pas l'auteur des Bidonchon, l'autre) pour calculer aisément les nombres de Fibonacci:
![]()
où Φ représente le nombre d'or (voir ci dessous), Φ' le conjugué du nombre d'or, c'est-à-dire les nombres:

F(n) peut être calculé comme l'entier le plus proche de :
![]()
Remarquons que ces deux formules donnent le terme F(n) d'une suite vérifient F(0) = 0, F(1) = 1, F(2) = 1, etc... c'est-à-dire que l'on a u(n) = F(n+1).
Il faut y penser pour vérifier les propriétés proposées au chapitre précédent.
Voici les sources qui permettent de calculer la suite de Fibonacci avec la méthode Binet Source de binet
Le triangle de Pascal
Parmi mes curiosités mathématique liées aux nombres de Fibonacci, l'une se rattache au fameux triangle de Pascale (Blaise, celui qui écrit quand il pense), que tout matheuphile paresseux connaît, puisqu'il permet de calculer les coefficients de la décomposition de (a+b)^n sans autres calculs qu'une série d'additions.
Additions dont le PC se chargera bien volontiers !
Rappelons que chaque terme du triangle est la somme des deux situés au dessus de lui :
1
1____1
1____2____1
1____3____3____1
1____4____6____4____1
1____5___10___10____5____1
1____6___15___20___15____6____1
Voici les sources qui affiche le triangle de pascal Source de pascal
On sait que la somme des termes d'une même ligne donne toujours 2^n: 1 = 2^0, 1 + 1 = 2^1, 1 + 2 + 1 = 2^2, 1 + 3 + 3 + 1 = 2^3, etc..
Si on effectue les sommes des termes selon les diagonales, on trouvera :
1 = 1
1 = 1
1 + 1 = 2
1 + 2 = 3
1 + 3 + 1 = 5
1 + 4 + 3 = 8
1 + 5 + 6 + 1 = 13
Vous aurez reconnu la suite de notre Léonard, sinon c'est à désespérer !
Or chacun des termes du triangle de Pascal est le nombre C(n,p): combinaison de n objets p à p, défini par: c(n, p) = n! / p!(n-p)! (n! signifie n(n-1)(n-2)...2.1), je vous laisse imaginer la belle formule que l'on peut écrire !.
Notons pour conclure ces propriétés (que les maths adorent) que les récents développements de l'informatique ont relancé l'intérêt pour ces suites parce qu'elles sont des applications pratiques dans le classement des données, la recherche des informations, la génération de nombre aléatoires, et certaines méthode rapides d'approximation des extrema de fonction compliquées dons les dérivées sont inconnues.
Pour briller en société (?), sachez enfin que la suite de Fibonacci intervient dans la démonstration du dixième de Hilbert (Vous savez le type aux sysygies ...)!
somme après somme, rapport après rapport, le nombre d'or
La propriété la plus connue de la suite de Fibonacci reste quand même celle concernant le rapport de deux termes consécutifs: quand n tend vers l'infini, le rapport: v(n) = F(n+1)/F(n) tend vers une limite, et cette limite est le nombre d'or.
Le nombre d'or, celui des mathématiciens et non celui des astronomes, est tout simplement la racine positive de l'équation: x²-x-1=0
Le calcul de Delta Egalbé de Moinquatrasset (vielle noblesse au second degré) nous donne les valeurs déjà citées Φ et Φ':

Mais pourquoi poser cette équation ? Au départ, pour établir une règle d'esthétique: partager l'unité en deux parties a et b afin que leur rapport a/b=x soit le même que le rapport de la plus grande au tout 1/a.
Or a + b = 1. donc:
(a + b)/a = x
1 + (b/a) = x
1 + (1/x) = x
et, en multipliant par x:
x + 1 = x²
Ce nombre d'or joue un rôle considérable tant dans l'analyse de phénomènes naturels que dans des branches très diverses des mathématiques, de la physique, de la biologie, et même dans des domaines où on ne s'attendrait pas à le trouver. Nous aurons l'occasion d'en reparler dans une prochaine rubrique... ou plusieurs, tant le sujet est vaste. Mais revenons au sujet du mois, les nombre de Fibonacci.
FI comme Physique
On donne le circuit électrique donné par le schéma ci dessous, où Ze désigne l'impédance d'entrée, Zs l'impédance de sortie, et An le rapport entre la différence de potentiel aux bornes de la sortie.

On a les valeurs suivantes:
n______: 1___2___3
Ze en Ω_: 2___5/3_13/8
Zs en Ω_: 1___2/3_5/8
An_____: 2___5___13
On établit par récurence:
Ze = F(2n + 1) / F(2n)
Zs = F(2n - 1) / F(2n)
An = F(2n + 1)
En optique.
Le nombre de rayons lumineux émergeant après un certain nombre de lames de verre à face parallèles est un nombre de Fibonacci.

BO comme botanique
Les branches, feuilles, fleurs ou graines sont assemblés et arrangées selon un certain motif général.
On y trouve souvent des nombres de Fibonacci:
Nombre de pétales des fleurs courantes:
La circée a deux pétales
L'iris, le lis, la tulipe ont trois pétales
Le bouton d'or,le delphinium, l'anémone, etc, ont cinq pétales
Delphinium, anémone, ficaire en ont huit (selon espèces)
Jacobée, camomille, marguerite en ont treize
Aster, chicorée, doronique: 21 pétales
Paquerette, marguerite des champs, plantain: 34 pétales
Aster d'automne: 55 ou 89 pétales
Ce motif n'est pas nécessairement suivi par toutes les plantes d'une même espèce, mais semble être une caractéristique de l'espèce.
Si des trèfles à quatre feuilles existent, ils sont pourtant moins nombreux que ceux dont le nombre de feuilles est F(4).
Position des feuilles le long d'une tige:
Les feuilles poussent régulièrement autour de la tige en décrivant des hélices.
En général, le nombre de feuilles nf entre deux feuilles placées directement l'une au dessus l'autre et le nombre de révolutions nr entre ces deux même feuilles sont des nombre de Fibonacci.
La mesure en nombre de tours de l'angle entre deux feuille est alors nf / nr.
Ainsi pour le tilleul et l'orme ce rapport est de 1/2, pour le hêtre et le noisetier 1/3, pour le chêne, l'abricotier, le cerisier 2/5, pour le peuplier et le poirier 3/8, pour le saule et l'amandier 5/13.
Le même angles est conservé pour une même espèce dans la disposition des branches, des fleurs et des bourgeons.
On constate en outre que les rapports les plus courants, 1/2, 1/3, 2/5, 3/8, 5/12, 8/21, ... sont de la forme F(n-2)/F(n), ce qui correspond à un nombre de tours voisin de 1/Φ².
Or, on démontre que pour toutes les feuilles, l'angle entre deux feuilles doit mesurer 1/Φ², (ou 1 / Φ selon l'orientation choisie, puisque 1/Φ² + 1/Φ = 1).
Spirales
Le coeur d'une fleur de tournesol ou de marguerite présente des graines réparties en spirales, l'une dans un sens, l'autre dans l'autre.
Le nombre de spirales dans chaque sens sont fréquemment des nombres de Fibonacci: 21 et 34, 34 et 55 ou 55 et 89 pour les fleurs de tournesol, 21 et 34 pour les marguerites.
On remarque le même phénomène pour les pommes de pin (3 et 5 ou 5 et 8 spirales) et pour les ananas (trois familles de spirales, puisque la structure n'est plus plane, de 5, 8 et 13 spirales.
Toutes ces règles souffrent des exceptions, mais apparaissent comme une tendance générale.
NA comme naturels (nombres)
Tout nombre entier se décompose en une somme de nombres de Fibonacci distincts.
De plus la décomposition est unique si l'on s'interdit deux nombres de Fibonacci consécutifs et si l'on prend les nombres de Fibonacci à partir de F(2), puisque 1 figure deux fois.
Cette propriété, qui porte le joli nom de théorème de Zeckendorf, nous replonge dans les maths.
Laissons de côté la démonstration - qui utilise la récurence - et bornons-nous à donner quelques résultats:
1 = 1
2 = 2
3 = 3
4 = 3 + 1
5 = 5
6 = 5 + 1
...................
25 = 21 + 3 + 1
46 = 34 + 8 + 3 + 1
88 = 55 + 21 + 8 + 3 + 1
Voici les sources qui calculent les suites ci-dessus Source de naturels
On peut s'intéresser au nombre d'éléments dans la décomposition de Fibonacci d'un nombre.
Ainsi, n(5) = 1, n(6) = 2, n(25)= 3, n(88) = 5, n(89) = 1, etc...
On obtient une loi récursive du plus bel effet.
Divisibilité: F(nk) est divisible par F(n) pour tout n et pour tout k.
Ça alors! Par exemple, F(5) = 5, F(10) = 55, F(15) = 610, F(20) = 6765: F(5) divise tous les autres, F(10) divise F(20).
Pour tout entier naturel n, il existe au moins un nombre de Fibonacci divisible par n parmi les n² - 1 premiers.
Par exemple, 6 divise F(12) et 12 < 36 ; 7 divise F(8) et 8 < 49.
Existe-t-il un nombre n qui divise seulement F(n²-1)?
A vos claviers!.
Voici les sources qui calculent les testes de divisibilités Source de divisible
C'est presque de la magie des nombres: Si F(n) est pair, alors n est divisible par 3, n est divisible par 4
Si F(n) est divisible par 5, n est divisible par 5
Si F(n) est divisible par 11, n est divisible par 10
Existe-t-il d'autres propriétés semblables ?
La réciproque de chacune est-elle vrai ?
A vos clef usb!
CCI comme a vos souhaits !
Vous n'êtes pas obligé de me croire, mais si on ne conserve que le chiffre des unités des nombres de Fibonacci, c'est-à-dire la suite a(n) = F(n) MOD 10, on obtient une série de 60 nombres qui se répète indéfiniment - une période, en quelque sorte.
Plus curieux, ce résultat est vrai pour toute suite de la forme a(n) = F(n) MOD k, où, k est un entier quelconque, la longueur de la période pouvant varier.
Exemples:
k = 2 Période 3: 0 1 1
k = 3 Période 8: 0 1 1 2 0 2 2 1
k = 4 Période 6: 0 1 1 2 3 1
k = 5 Période 20.................... à vous de jouer !
Je vous recommande particulièrement k = 30 (période 120), k = 98 (période 336), k = 125 (période 500).
Voici les sources qui calculent a(n) = F(n) MOD 60 Source de 60
Voici les sources qui calculent a(n) = F(n) MOD k Source de periode
On pourrait discourir encore longtemps sur les tours et détours de Léonard de Pise et de ses nombres, dont l'inventeur n'avait sous doute pas mesuré l'étendue des propriétés.
Ajoutons que Lucas - le "découvreur" à également laissé son nom à une suite similaire, définie de la même façon mais dont les premiers nombres sont 1 et 3.
Le propriétés des nombres de Lucas sont aussi nombreuses que celles des nombres de Fibonacci, qu'elle recoupent souvent.
Nous en reparlerons prochainement, et parlerons plus longuement du nombre d'or dont il ne faudrait pas faire phi (pardon fi)!
Un grand merci à MM Meyer et Steyaert pour leur remarquable documentation, à André Déledicq mon respectueux hommage, ainsi qu'à toute l'équipe de l'IREM de Paris VII, à Martin Gardner l'assurance de ma lucidité, et à tous les lecteurs et lectrices de ST Mage, salut !
Jean Pascal Duclos