Fibonacci partie 2

Table des matières

1. La reine coincée et les petits chinois.
2. Un jeu passé au crible.
3. jeu de Nim : cases gagnantes.
4. Des couples qui se séparent...
5. Une propriété en or
6. Fibonacci, Fibona-là
7. Bizarre autant que tranches
8. L'état de décomposition de Fibonacci est avancé
9. Le discours de la méthode
10. Demandez le programme!
    Les sources du chapitre entier avec son Makefile Sources
    

La reine coincée et les petits chinois.

O grands ludiques que vous êtes vous vous doutez bien que toute théorie des nombres trouve des retombées dans la théorie des jeux, et que les pérégrinations de notre Léonard, Bonacci sans pour autant être bon à rien, serviraient à toute autre chose qu'à faire des mathématiques.
Edouard Lucas lui-même , l'inventeur de Fibonacci, n'est-il pas connu autant pour ses ouvrages de récréations mathématiques que pour son apport à la théorie des nombres?
L'un des jeux les plus simples est le jeu de Nim, dont il existe de nombreuse variantes, en particulier le fameux jeu de Marienbad..
... un jeu auquel je gagne toujours... je peux perdre, mais je gagne toujours.
...je trouve ce jeu absurde... c'est un truc à connaître... il suffit d'en prendre un nombre impair... il y a des règles, sûrement... c'est celui qui commence qui perd... je me rappelle que Franck jouait à ça, l'année dernière... prendre à chaque fois le complémentaire à sept... c'est celui qui commence qui gagne... il faut en prendre un nombre pair... le plus petit nombre impair total... c'est une série logarithmique... changer de rangée à chaque fois... diviser par trois... sept fois sept quarante-neuf...
Petit exercice: parmi les affirmations précédentes -toutes dans le film de Resnais- lesquelles contiennent un embryon de réponse?
On sait depuis longtemps que la solution utilise la décomposition de nombre dans le système binaire, réservé à cette époque épique à quelques rares informaticiens et à une foule de manipulateurs d'allumettes.
Dans le jeu suivant, très proche de celui de l'année dernière, on rencontrera derrière quelques allumettes les suites de Fibonacci:
On dispose deux tas (de préférence différents, car si les tas ont le même nombre d'éléments, le jeu est immédiat) d'objets divers: allumettes, pièces de monnaie, cartes, vieux numéro de ST MAG, etc..
Chaque joueur joue à son tour et peut :
- Soit retirer d'un tas autant d'objets qu'il lui plaît,
- Soit retirer autant d'objets dans un tas que dans l'autre.
Vous aurez bien entendu reconnu le jeu favori des petit chinois, pratiqué depuis des millénaires sous le nom de tsyanshidzi, ce qui ne veut pas dire "A vous souhait" mais "Choisis la pierre".
Une variante de ce jeu consiste à placer une reine sur un échiquier sur une case de son choix. Chaque joueur à tour de rôle déplace la reine, mais seulement vers la gauche ou vers le bas.
Le vainqueur est celui qui parvient à amener la reine sur la case du coin en bas et à gauche de l'échiquier, où elle est irrémédiablement coincée.
L'échiquier peut êtres rectangulaire si le coeur vous en dit.

Un jeu passé au crible.

Si on représente la configuration du jeu par un couple d'entiers (x, y), où x et y représente le nombre d'objets de chaque tas, on voit que le jeu consiste à remplacer le couple (x, y) par l'un des couples (x-k, y), (x, y-k) ou encore (x-k; y-k), le nombre k étant choisi pour que les soustractions donnent un nombre non-négatif (au moins nul).
Étudions les configurations perdantes: il est clair que pour gagner, il faut laisser à l'adversaire le couple (0, 0), puisque l'on a ramassé le dernier objet.
Or ce couple n'a pu êtres atteint que si l'on part d'un couple (k, 0), (0, k), ou (k,k).
Si l'on représente graphiquement l'ensemble des couples par un quadrillage , cela revient à hachurer la ligne, la colonne et la diagonale contenant une case favorable.
Toutes case hachurée devient donc une case défavorable (...de lapin, puisque Fibonacci n'est pas loin!).
Toute case non hachurée devient donc favorable, et on recommence de proche en proche.
Le procédé n'est pas sans rappeler la méthode du crible d'Erathostène pour la détermination des nombre premiers, et elle ne donne qu'une partie des solutions.
On obtient le diagramme suivant:

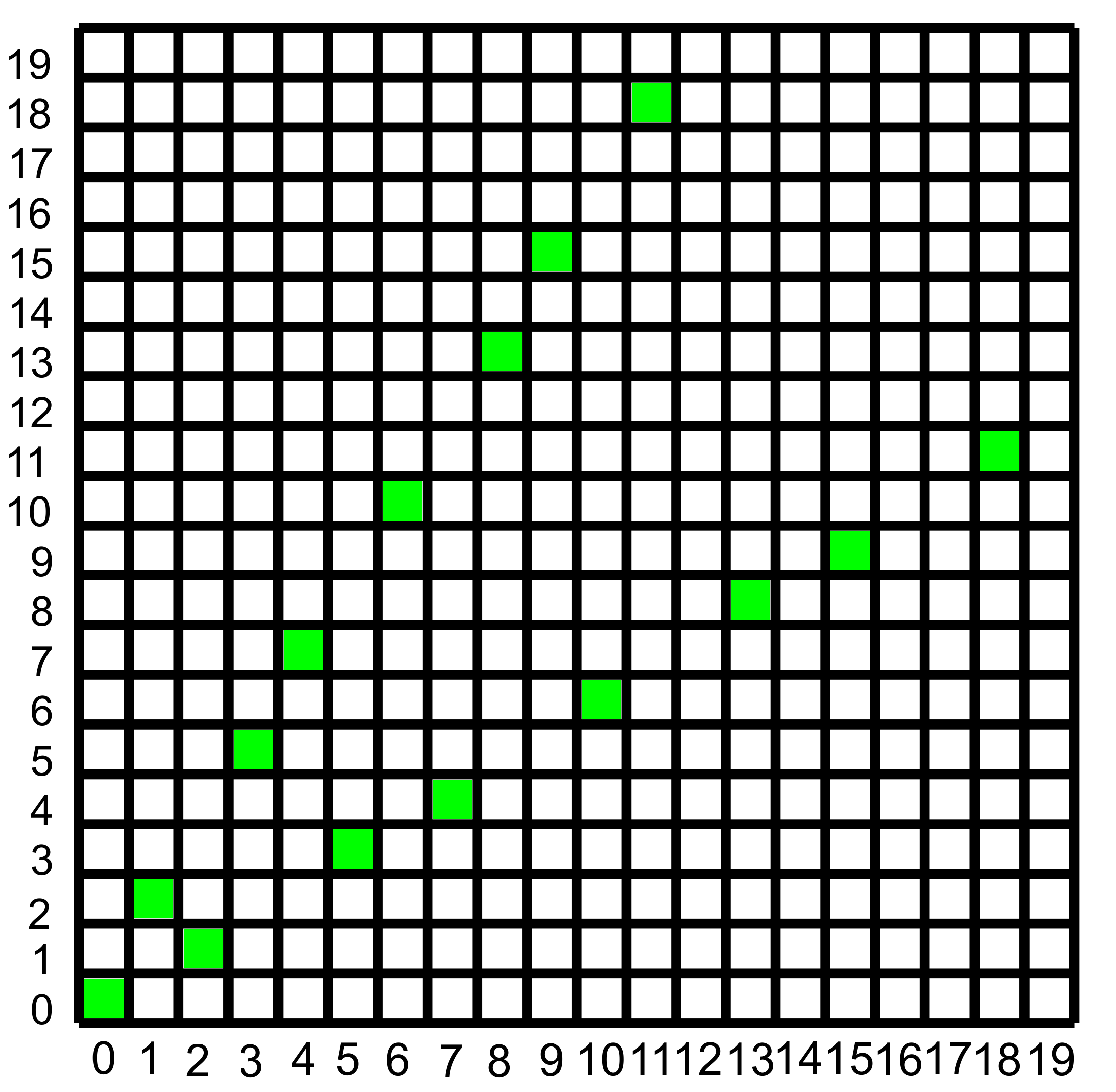
jeu de Nim : cases gagnantes.

En ordonnant par rapport aux abscisses croissantes ces couples, on obtient la suite de couple (0, 0), (1, 2), (3, 5), (4, 7), (6, 10),... c'est-à-dire deux suite associés, u=0, 1, 3, 4, 6... et v= 0, 2, 5, 7, 10...
L'étude jusqu'au rang 15 donne les résultats suivant:
n=1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
a=1 3 4 6 8 9 11 12 14 16 17 19 21 22 24
b=2 5 7 10 13 15 18 20 23 26 28 31 34 36 39
Un grand nombre de mathématiciens de tous poils se son consacrés à l'étude de ces suites, tant en Europe qu'aux Etats-unis.
A l'étude de ce jeu reste attaché en premier lieu le mathématicien hollandais W.A Wythoff, qui en publia une analyse en 1907.
Si l'on n'étudie que les couples (a, b) où a < b, c'est que l'on aura remarqué que la configuration est symétrique par rapport à la bissectrice: si (a, b) est favorable, (b, a) l'est aussi.

Des couples qui se séparent...

La première remarque que l'on peut faire en observant l'ensemble des couples (a, b), c'est la différence b-a, non seulement devient de plus en plus grande, mais augmente d'une unité à chaque rang:
0 - 0 = 0
2 - 1 = 1
5 - 3 = 2
7 - 4 = 3
.........
En autres termes, si on l'on connaît a(n), on obtient b(n) en ajoutant le rang n du couple considéré : b(n) = a(n) + n.
Cette remarque permet de trouver un algorithme de construction des couples favorables (a, b) de proche en proche:
Pour a, on prend le premier entier non encore utilisé dans une construction antérieure.
b est alors égal à a + n.
On perçoit immédiatement le peu d'aisance de cet algorithme en ce qui concerne éventuelle programmation sur votre Sensuelle Tentatrice (la puce de votre ordinateur!) .
Pour le choix du nombre a, il faut tester les 2n - 2 couples précédant le couple de rang n - et encore, si l'on néglige le couple (0, 0).
Il faudra donc chercher autre chose... mais ce ne sont pas les propriétés curieuse qui manquent.
Cependant, cette construction met en relief une propriété intéressante: tout entier est soit un nombre b, soit un nombre a.
Seul zéro appartient aux deux catégories.
Cette propriété se traduit par le fait que sur le diagramme, chaque ligne contient une case favorable et une seul (il en est évidemment de même pour les colonnes, par symétrie).
Il est donc possible de passer n'importe quel couple (x, y) à un couple favorable (a, b) en modifiant l'une des coordonnées... sauf si l'on est sur case favorable que l'on doit quitter à cause de l'obligation de jouer!.
Il n'y a plus à espérer alors que votre adversaire ne lise pas ST Mag... et jouer petit en attendant de voir venir!
Une autre propriété étonnante des couples (a, b):< br/> 1 + 2 = 3 ---> a(2) = 3
3 + 5 = 8 ---> a(5) = 8
4 + 7 = 11 ---> a(7) = 11
Ça alors ! la somme a + b (pour un rang quelconque) donne le terme a de rang b!
Si cela est, c'est donc que le b de rang b est égal à a + 2b, puisque b = a +n!.
Bon sang mais c'est bien sûr! (une aspirine, un verre d'eau, et on relit tout ça calmement...).

Une propriété en or

Il existe cependant une méthode pour construire ces deux suite de manière non récurrente, c'est à dire que l'on peut calculer a et b au rang n sans avoir calculé tous les termes précédents.
W. A. Wythoff fut le premier à remarquer que les nombres a sont en fait les parties entières des multiples consécutifs du nombre d'or (tiens, le revoilà).
Il affirme avoir fait fait cette découverte par hasard, comme un magicien tire un lapin - sans nul doute de Fibonacci - de son chapeau.
Ce nombre d'or alias Racine-de-cinq-plus-un-sur-deux, matricule 1.61803398... se retrouve encore ici :
Cette fois, le calcul de a est immédiat par un programme : Source de nimA
Pour le calcul de b, on peut utiliser b = a + n.
Mais il y a plus fort: chaque b est la partie entière des multiples du carré du nombre d'or.
Ça vous épate? c'est pourtant simple: si k désigne le nombre d'or, on a k^2 = k + 1.
Donc n*k^2 = n*k + n.
On en déduit que int(n*k^2) = int(n*k)+n.
C'est fou!
en résumé:
a(n) = int(n*k)
b(n) = int(n*k^2)
Voici un programme qui calcul a et b suivant les formules ci-dessus : Source de nimAB
Le nombre d'or n'est pas le seul à engendrer des suites complémentaires (mais il est le seul à engendrer des suites de Wythoff).
En fait, tout nombre irrationnel x (racine de deux, pi, e, ...) engendre deux suite a et b complémentaire définie par:
a = int(n * x)
b = int ((n * x) / (x - 1))
si x est le nombre d'or 1/x = x - 1, c'est pourquoi l'on trouve k^2.
Cette propriété n'est pas vraie si x est un rationnel (de la forme m / p où m et p sont entiers).
Si x = 3, les premiers termes sont a=[3] = 3, b = [3/2] = 1, puis a = [6] = 6, b = [6/2] = 3, puis a = [9] = 9 et b = [9/2] = 4.
3 figure dans les deux suites 2 dans aucune.
Si x = 5/3, on trouve comme premiers couples (1, 2), (3, 5), (5, 7),..
On remarque que 5 figure dans les deux suites, et, les deux suites étant croissantes, que 4 ne figure nulle part.

Fibonacci, Fibona-là

On aura remarqué que les premières valeurs de a et b sont des nombres de Fibonacci (Comment? vous ne savez pas ce que c'est. Vous êtes démasqué! Lisez d'urgence le chapitre précédent pour y relire les aventures de l'ami Fibo!).
Hélas,à partir du rang 3, ça se gâte.
4 et 7 ne sont pas des nombres de Fibonacci.
Les plus avisés d'entre vous reconnaîtront peut-être des nombres de Lucas (les nombres de Lucas vérifient la loi de la formation u(n) = u(n - 1) + u(n - 2), mais les nombres de départs sont différents: 2 et 1)/
Mais la propriété plus haut énoncée nous permet d'affirmer que tous les couples formés par deux nombres de Fibonacci consécutifs à partir de 1, 2 en respectant le rang (le couple 3, 5 convient, mais pas 2, 5 ni 5, 8) donnent des couples favorables.
En effet, on a vu que a(b) = a + b.
Si a et b sont deux nombres consécutifs de Fibonacci, a(b) est le suivant de la suite.
De plus b(b)=a(b)+b, donc b(b) est le terme suivant dans la suite (Fn).
Et voilà!

Bizarre autant que tranches

Donc, pour trouver certains couples de favorables, on écrit la suite de Fibonacci généralisée (c'est-à-dire que chaque terme est la somme des deux termes précédents) engendrée par le premier couple, et on découpe cette suite en tranche de deux termes.
Chaque tranche nous donne un couple de Wythoff.
On recommence avec le premier couple non atteint par cette suite, et on réitère.
1_2__/_3__5__/_8__13__/_21_34_/_....
4_7__/_11_18_/_29_47__/_....
6_10_/_16_26_/_42_68__/_....
9_15_/_24_39_/_63_102_/_....
........
On distingue donc un ensemble de germes :(1, 2), (4, 7), (6, 10), (9, 15),... qui donnent chacun une infinité de couples favorables.
Relevons le rang de chacun de ces germes:
On trouve dans l'ordre 1, 3, 4, 6,...
Je n'en crois pas mes yeux! C'est la suite des a!!!
Et en plus, ce n'est même pas une coincidence: il paraît que ça se démontre, et qu'un certain Silber a énoncé le théorème suivant:
Un couple de Wythoff est un germe si et seulement si son rang appartient à la suite des a(n).
Vous avez le droit d'aller vous chercher une deuxième aspirine (sachez apprécier avec modération).

L'état de décomposition de Fibonacci est avancé

Si votre passion pour l'informatique vous laisse encore quelques loisirs, vous avez peut-être lu jusqu'au bout le premier chapitre, et avez découvert avec surprise que la suite de Fibonacci permet de décomposer n'importe quel entier en somme de termes de cette suite.
Ainsi,
14 = 13 + 1
31 = 21 + 8 + 2, etc...
Ce qui est remarquable dans cette décomposition, c'est quelle n'utilise jamais des termes consécutifs... forcément, sinon on pourrait les remplacer par leur somme, qui est aussi un terme de la suite!
On peut donc associer à tout nombre entier une suite de 0 ou de 1, le calcul se faisant comme pour, au hasard, le système binaire...
Par exemple:
55_34 21 13 8 5 3 2 1 1
1 0 0 0 1 0 0 0 1 0 donne 64
On remarquera que le fit (fibonaccirydigit) de droite est toujours à zéro puisqu'il est doublé par son voisin de gauche.
On sait qu'en binaire, si l'on écrit un zéro à droite de l'écriture d'un nombre, on obtient l'écriture du double de ce nombre.
De même, si l'on supprime le zéro de droite, on divise ce nombre par deux par un simple jeu d'écriture.
Si l'on fait subir les mêmes métamorphoses à la décomposition d'un nombre en notation de Fibonacci, le résultat est loin d'être évident: 5 devient 8, 14 devient 23, la loi de transformation associée à cette fibo-multiplication semble bien chaotique!
Et pourtant, cette opération de décalage va se révéler être un outil puissant pour la détermination des paire de Wythoff.

Le discours de la méthode

Appelons FG l'opération consistant à ajouter un zéro à droite de l'écriture, donc à décaler la suite de 0 et de 1 d'un rang vers la gauche (ce qui en binaire correspondrait à une multiplication par 2), et FD l'opération consistant à enlever le zéro de la droite (équivaut en binaire à la division par 2... je veux dire &X10).
La table de multiplication est curieuse :
FG(1)=2; FG(2)=3; FG(3)=5; FG(4)=7; FG(5)=8; FG(6)=10; FG(7)=11 ;FG(8)=13...
Mais je rêve: les couples n, FG(n) sont, pour la plupart d'entre eux, des couples de Wythoff!
Eh oui... la décomposition de Fibonacci permet de se faufiler d'une case favorable à l'autre!
La mathématicien américain Robert Silbert propose cette méthode:
Soit (x, y) un couple quelconque tel que x<=y.
On établie la décomposition de Fibonacci x : selon que le premier 1 en partant de la droite sera pair ou impaire, x sera de type a ou de type b : première composant ou deuxième composant d'un couple de Wythoff (On a forcément soit l'un, soit l'autre).
Ainsi, pour la suite a, on obtient:
suite a________suite b
1 = 10_________2 = 100
3 = 1000_______5 = 10000
4 = 1010_______7 = 10100
6 = 10010_____10 = 100100
8 = 100000____13 = 1000000
9 = 100010____15 = 1000100
11 = 101000___18 = 1010000
Cette remarque permet de savoir si un nombre x donné sera un terme de la suite de b.
On remarquera dans ce tableau que pour tout couple a, b on a la relation b = FG(a).
On peut donc savoir si un couple (x, y) est ou non un couple favorable: si x appartient à la parité a, et si b = FG(a), la case (x, y) est une case favorable... à condition de pouvoir l'atteindre.
Elle est défavorable si l'obligation de jouer vous oblige à quitter cette case.
Il faut alors jouer au hasard, en attendant une erreur de l'adversaire.
Une case (x, y), non favorable, étant occupée, comment peut-on atteindre une case favorable?
Ici encore, Silber propose son algorithme basé sur la décomposition de Fibonacci (on suppose que x < y):
1) Si x est de parité b, on calcul FD(a), qui nous donne la valeur de y à obtenir:
Ex (10, 15): 10 = 100100, de parité b.
FD(10) = 10010 = 6
On cherchera à atteindre la case (10, 6) qui est favorable, en retranchant 15 - 6 = 9 objets au deuxième tas.
2) Si x est de parité a, deux cas peuvent se produire:
a) On calcul FG(x).
Si FG(x)<y, on peut diminuer le tas y pour obtenir FG(x), et on a donc une case favorable.
Ex (9, 20): 9 = 100010, parité a
FG(9) = 1000100 = 15
Comme 15 < 20, on peut retrancher 5 objets au deuxième tas pour passer du couple (9, 20) non favorable au couple (9, 15) favorable.
b) Il se peut pourtant que FG(x) soit plus grand y:
On utilise alors la deuxième règle du jeu: Tout d'abord, on calcule la différence y-x = d, et c'est sur d que porte l'algorithme :
On calcul d-1, puis la décomposition de Fibonacci de ce nombre.
On change alors le zéro de la droite en 1.
On obtient bien une décomposition de d, mais impropre puisque le nombre de droite n'est pas zéro, et que deux 1 peuvent êtres consécutifs.
On calcul alors a en écrivant un zéro à droite, et b en écrivant un deuxième:
Les décompositions obtenues peuvent êtres impropres, mais sont néanmoins calculables.
Exemple: soit le couple (24, 32): 24 = 10001000, donc de parité a
FG(24) =100010000 = 39 Comme 39 est plus grand que 32, la méthode du a) ne peut s'appliquer.
On calcule d = 32 - 24 = 8
7 = 10100, donc 8 = 10101
(décomposition irrégulière)
FG(8) = 101010 = 12
FG(12) = 1010100 = 20
Le couple favorable à obtenir est donc (12, 20)
Il s'obtient en retirant 12 objets à chaque tas.

Demandez le programme!

Les programmes donnés permettent d'illustrer les propos arides de cette page:
Tout d'abord un programme qui donne la décomposition de Fibonacci d'un nombre de votre choix, non pas avec des zéros et des uns, mais en entourant avec < et > dans la suite complète les termes concernés.
Le résultat est plus lisible, et permet de calculer mentalement les FG et FD.
Voici le source Source de decomposition
Un programme vous donne un grand nombre de suites de Wythoff, avec leur rang,ce qui vous permettra de vérifier les propriétés nombreuses proposées plus haut.
Voici le source Source de wythoff
Le troisième programme, enfin, vous propose une partie de tsyanshidzi où vous êtes assurés de perdre si vous ne gagnez pas une configuration favorable.
Pour vous laisser une petite chance, l'ordinateur jouera de temps en temps au hazard, selon une probabilité que vous pourrez modifier vous même.
Voici le source Source de tsyanshidzi
Un petit mot sur le monstre mathématique limitant l'étude de la suite de Fibonacci :
On sait que Fn est l'entier le plus proche de (phi^n/sqrt(5)).
Il faut déterminer n afin que Fn soit le plus grand q'un nombre donné A, mais pas trop.
Les propriétés des logarithmes permettent d'écrire:
Log(phi^n) = n * Log(phi)
Log(sqrt(5)) = 0.5 * Log(5)
Log(x/y) = Log(x) - Log(y)
(Notations utilisées en informatique)
Ces relations permettent d'établir la formule déterminant le calcul de Mf: rang maximum d'étude de la suite de fibonacci.
Et si tout cela vous parait trop aride, sachez qu'il existe une variante au jeu Coincez la Reine où cette dernière est remplacée par une bulle.
Nous laissons à chaque lecteur le soin d'en définir les règles et les stratégies.
Jean Pascal DUCLOS

Revenir au haut de la page