Fibonacci partie 3

Table des matières

1. Fibonacci et les jeux (suite).
2. Le nombre d'or.
3. Le nombre d'or et l'algèbre.
4. expressions du nombre d'or.
5. le nombre d'or et la géométrie.
6. Nombre d'or, dodécagone et pentagones.
7. Triangle d'or, rectangle d'or.
8. Les arts et le nombre d'or.
   Les sources du chapitre entier avec son Makefile Sources
   

Fibonacci et les jeux (suite).

Post-scriptum au numéro précédent: si d'aventure votre négociant en tabac n'a pas encore distribué tout son stock d'allumette aux lecteurs de ce site, vous pouvez vous entraîner au petit jeu que je vous propose: On dispose cette fois d'un tas unique d'allumettes, chaque joueur joue à tour de rôle en respectant les règles suivante:
Au premier tour, le premier joueur ramasse autant d'allumettes qu'il désire, mais doit en laisser au moins une.
Aux tours suivants, on peut par contre ramasser tout le tas si la deuxième règles le permet:
Chaque joueur ramasse ensuite autant d'allumette qu'il veut - au moins une - mais pas plus que le double du précédent ramassage.
Supposons que A ait ramassé 12 allumettes au tour précédent, B peut ramasser entre une et 24 allumettes.
Le vainqueur est celui qui ramasse la dernière allumette.
Croyez-moi si vous voulez, cette variante du jeu de Nim utilise encore la décomposition d'un entier en nombre de Fibonacci.
On montre que si le nombre d'éléments du tas est un nombre de Fibonacci, le second joueur gagne à coup sûr.
Sinon, c'est le premier joueur qui gagne.
L'astuce consiste à enlever le plus petit nombre de Fibonacci présent dans la décomposition de n:
Par exemple, n = 20, 20 n'est pas un nombre de Fibonacci.
Donc le joueur peut gagner.
La décomposition de 20 en nombres de Fibonacci est 20 = 13 + 5 + 2.
Il faut donc retirer deux éléments au tas, qui en contiendra alors 18.
Comme le joueur suivant ne peut retirer plus de quatre éléments, il ne pourra atteindre 13, nombre de Fibonacci immédiat inférieur à 18.
Voici le source du jeu de cette variante de Nim varianteNim
Pour revenir sur le jeu des deux tas, on peut jouer avec la variante qui perd-gagne: celui qui ramasse la dernière allumette est perdant.
Il n'est pas nécessaire de reprendre toute la stratégie: c'est la même! Les seules modifications concernent les trois premières cases: 0,0; 1,2 ; 2,1 sont à remplacer par 2,2 ; 0,1 ; 1,0.
Vous êtes assez grand pour modifier le programme afin de proposer les deux variantes, aux choix (si l'on veut, puisque l'on perd toujours!).
Voici le source (ne marche pas bien) de la version modifiée de tsyanshidzi tsyanshidzi2
Et pour conclure l'apport de Fibonacci dans la théorie des jeux, un petit tour de passe-passe:
On demande à deux personnes de l'aimable assemblée de choisir deux nombres, notés en colonne sur une feuille de papier.
On écrit en dessous la somme de ces deux nombres, puis la somme des deux derniers nombre inscrit, comme on fait pour calculer les termes d'une suite de dix nombres.
Un simple coup d'oeil à la feuille permet de calculer mentalement la somme des dix nombre inscrits.
Le truc consiste à multiplier par 11 le septième nombre inscrit, ce qui se fait facilement en ajoutant de proche en proche deux chiffres consécutifs, et en tenant compte des retenues.
Par exemple, 486 donne 6 + 0 = 6 ; 8 + 6 = 14 ; 4 + 8 = 12 (plus retenue: 13) ; 0 + 4 = 4 (plus retenue: 5).
Donc 486 * 11 = 5346.
Pour l'explication de ce tour, il est facile de montrer que si a et b sont les deux premiers nombres, le septième vaut 5a + 8b, et la somme des dix 55 a + 88 b. CQFD!

le nombre d'or.

Quand on manipule une suite de Fibonacci, nous l'avons vu, le nombre d'or n'est pas loin.
Rappelons que le nombre d'or est défini par (1 + sqr(5))/2, désigné en général par la lettre grecque PHI (hommage au sculpteur Phidias - qui vaut mieux que l'opérette Phi-Phi écrite en son honneur (?)).
On montre que, pour toute suite de Fibonacci généralisée (c'est-à-dire telle que Un = U(n-1) + U(n-2), U1 et U2 arbitraires), le rapport de deux termes consécutifs se rapproche de Phi quand n croît.
En effet; soit Xn le rapport U(n-1)/Un.
Le terme X(n+1) aura pour valeur 1 + 1/X.
Cette suite est constante si Xn - X(n+1), c'est à dire si Xn est racine de l'équation:
X^2-X-1=0 (1)
dont les racines sont le nombre d'or PHI, et l'opposé de son inverse, PHI1, dont la valeur est (1 - Sqr(5))/2.
Notez qui si l'on calcul Xn à partir de la valeur PHI, votre ordinateur ne proposera pas une suite constante, mais que la suite convergera vers PHI.
Voici le source de convergence vers Phi convergencePhi
Cela tient du fait que pour PHI, la suite obtenue est constante, mais que pour toute autre valeur, elle convergera vers PHI.

le nombre d'or et l'algèbre.

Le mystérieux nombre d'or est donc simplement défini par PHI^2 = PHI + 1.
Cette propriété partagée par PHI1, permet de construire un grand nombre de propriétés algébriques:
La condition fondamentale permet d'écrire PHI = 1 + 1/PHI, nous l'avons vu.
On tire de cette relation la propriété:
PHI - 1/PHI = 1
La différence entre le nombre d'or et son inverse est égale à 1.
C'est à dire que les parties décimales de PHI et de son inverse sont rigoureusement identique:
PHI = 1,61803
1/PHI = 0,61803
Cette particularité étonne et séduit.
En fait, c'est une propriété partagé par toute racine d'une équation de la forme x^2 - nx -1 = 0.
Par exemple, (1 + sqr(2)), racine de l'équation x^2 - 2x -1 donne:
(1 + sqr(2)) = 2,1414...
1/(1 + sqr(2)) = 0,1414...
Pour le nombre d'or, cependant, prend la valeur la plus simple possible: n = 1.
Cette propriété permet de simplifier certains calculs: au lieu de diviser par PHI, on multiplie par PHI-1.
La relation fondamentale permet de montrer:
PHI^3 = PHI^2 + PHI
PHI^4 = PHI^3 + PHI^2
......... PHI^n = PHI^(n-1) + PHI^(n-2)
Cette propriété est également partagée par PHI1.
Conclusion: Une suite géométrique de raison PHI vérifie la propriété de Fibonacci.
Il en est de même d'une suite géométrique de raison PHI1.
toute suite de Fibonacci peut s'écrire sous la forme:
Un = a * PHI^ n + b * PHI1^ n (2)
a et b étant déterminés par les conditions initiales.
Le cas a = 1 et b = 1 donne la suite 2, 1, 3, 4, 7,... des nombres de Lucas.
La propriété (2) montre que Un/U(n-1) tend vers PHI quand n augmente indéfiniment, et vers PHI1 si n n'augmente indéfiniment par la valeurs négatives.

Expressions du nombre d'or.

De la propriété (1), on tire, nous l'avons vu, PHI = 1 + 1/PHI.
Si l'on considère la suite U1 = 1, et Un = 1 + 1/U(n-1), on obtient un développement de PHI en fraction continue:
U1 = 1
U2 = 1 + 1/1 = 2
U3 = 1 + (1 + 1/1) = 3/2
U4 = 1 + (1 + 1/(1 + 1/1)) = 5/3
PHI = 1 + (1 / (1 + 1/ (1 + 1/(......))))
Expression dans laquelle intervient un nombre infini de fois le nombre 1.
Notons que les premières valeurs donnent les rapports de deux termes de Fibonacci consécutifs.
De l'équation (1), on peut aussi tirer PHI = Sqr(1 + PHI).
Donc (en remplaçant la deuxième apparition de PHI):
PHI = Sqr(1 + Sqr(1 + PHI))
et, en réitérant: PHI = Sqr(1 + Sqr(1 + Sqr(1 + Sqr(1 + .....))))
Cette fois encore, on utilise le nombre 1 uniquement un nombre infini de fois.
On peut aussi montrer que:
PHI = 1 -1(1*2) +1/(2*3) -1/(3*5)...
(1 + (-1)^n/Fn^2)...

Le nombre d'or et la géométrie.

Le nombre d'or se prêtre à merveille aux exercices des virtuoses du compas.
A partir du nombre d'or, il est possible de créer une grande variété de formes et de figures géométriques, qui séduisent non seulement l'esprit mais encore le sens visuel.
A une esthétique de l'esprit s'ajoute une esthétique visuelle, en liaison directe avec l'instinct.
On retrouve d'ailleurs le nombre d'or, ou des valeurs approchées, dans un grand nombre d'oeuvre picturales ou architecturales (nous verrons qu'il est également présent dans des oeuvres musicales ou littéraires).
Pour les mathématiciens grecs de l'antiquité, l'existence d'un nombre est directement lié à la possibilité de sa représentation graphique, c'est-à-dire que tout nombre est la mesure d'un segment que l'on peut tracer.
Ce qui explique les abîmes de perplexité où se trouvent plongés les malheureux voulant représenter certains nombre dont on conçoit l'existence, mais dont toute tentative de représentation échoue, le nombre PI étant l'exemple le plus typique.
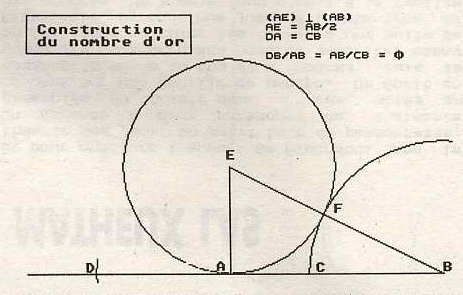
Tous les tracés utilisent le théorème de Pythagore, le nombre sqr(5] étant représenté par l'hypoténuse d'un triangle rectangle de respectifs 1 et 2, donc d'un tracé assez simple.
Les figurent ci-dessous donnent quelques méthode pour obtenir la la proportion dorée, c'est-à-dire deux segments dont le rapport des longueurs est égale au nombre d'or.

Nombre d'or, dodécagones et pentagones.

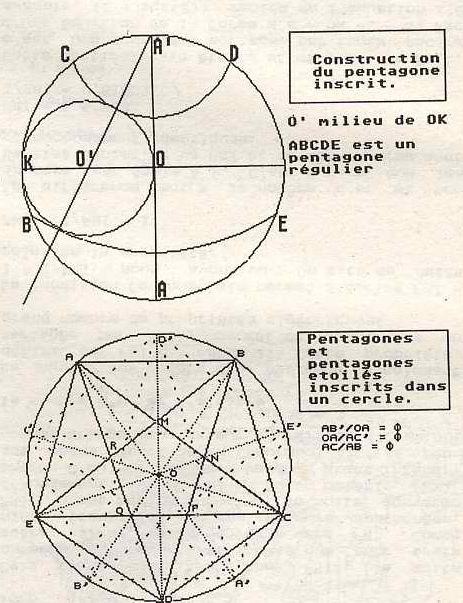
En géométrie, le nombre d'or est très lié au pentagone régulier inscrit et au pentagone étoilé.
Peut-être faut-il chercher là la réputation magique attribuée au pentacle, figure formée d'un pentagone étoilé inscrit dans un cercle.
Les cotés respectifs du pentagone régulier et du pentagone étoilé inscrit dans cercle de rayon 1 sont CR= sqr((5 - sqr(5))/2) et CE= sqr((5 + sqr(5))/2), et on montre que CE/CR = PHI.
Pour tracer tracer le pentagone régulier, plusieurs méthodes sont possibles.
Le tracé ci-dessous est le plus courant.
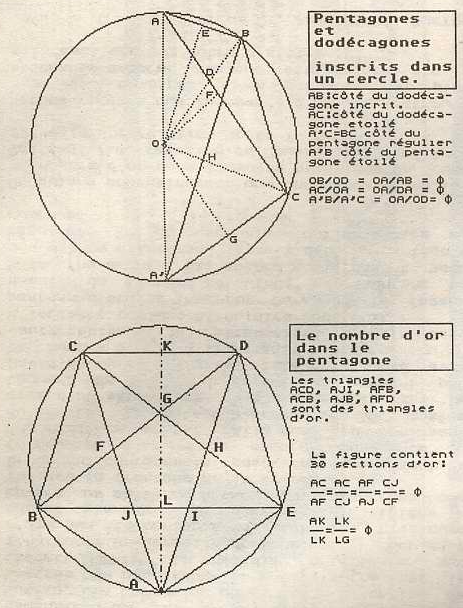
Pour tracer le dodécagone, on trace deux pentagones.
En traçant les droites caractéristiques des pentagones et des dodécagones, réguliers et étoilés, on fait apparaître un grand nombre de fous le rapport PHI.

Triangle d'or, rectangle d'or.

Le triangle d'or est un triangle dont les cotés vérifient de près ou de loin la proportion dorée.
Ce sont en fait des triangles apparaissant dans le pentagone convexe, le pentagone étoilé, les décagones convexe ou étoilé.
Les angles mesurent 18°, 36°, 54°, 72°, 108°, 126°, 144°.
On retrouve PHI dans l'expression des valeurs trigonométriques de ces angles:
sin 18° = 1 / (2 * PHI)
cos 18° = sqr(PHI +2) / 2
sin 36° = sqr(3 - PHI) / 2
cos 36° = PHI / 2
Certains triangles d'or sont isocèles.
Il en est de quatre type: (72, 72, 36) ; (36, 36, 108) ; (54, 54, 72) ; (18, 18, 144) - les nombres sont les mesures des angles du triangles.
D'autres triangles sont rectangles: (18, 72, 90) ou (36, 54, 90).
Plus connu et plus répandu, le rectangle d'or est un rectangle dont les cotés ont un rapport égal à PHI.
Mais le nombre d'or intervient dans un grand nombre de rectangles dorés, où PHI représente par exemple le rapport de la diagonale à la longueur (triangle égyptien), ou de la longueur à la demi-diagonale, ou à la pseudo-médiane joignant un sommet au milieu d'un coté opposé.
Le rectangle Parthénon (devinez pourquoi on l'a ainsi nommé!) présente un rapport entre la diagonale et la pseudo-médiane égale à PHI.
La figure montre un certain nombre de ces triangles:

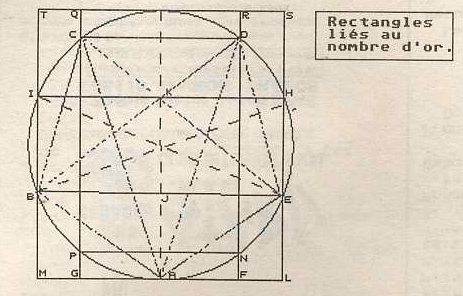
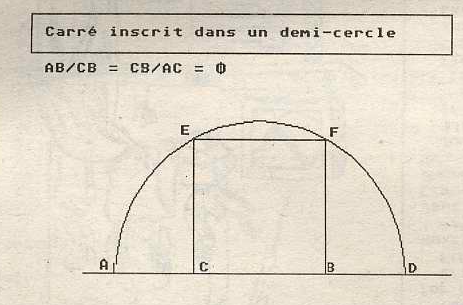
Le nombre d'or intervient dans un grand nombre de constructions géométriques comme par exemple l'inscription d'un carré dans un demi-cercle (voir figure).

Mais la propriété la plus curieuse du rectangle d'or est liée à la relation PHI^2 = PH + 1.
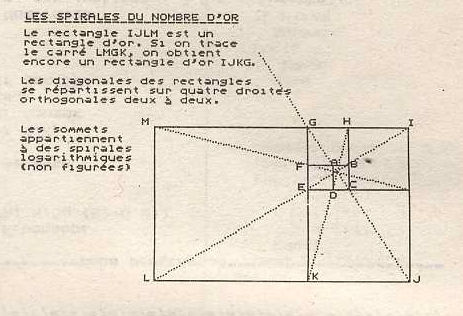
Si l'on découpe dans un rectangle d'or un carré, le rectangle restant est encore un rectangle d'or.
Plus curieux encore, on peut construire une figure comportant des rectangles d'or successifs (et leurs carrés associés). Sur une telle figure (voir ci-dessous) les sommets appartiennent à des spirales d'Archimède.
Une spirale d'Archimède, ou spirale logarithmique, est une spirale dont l'angle croit selon une progression arithmétique, alors que le rayon croit selon une progression géométrique.
La relation entre la longueur et la direction du rayon vecteur est donc logarithmique.

Les arts et le nombre d'or.

Le nombre d'or a de tous temps été utilisé par les artistes, de manière consciente ou inconsciente, en raison de ses qualités esthétique.
On pense que la division d'or d'un segment est la plus agréable à l'oeil.
En photographie, par exemple, on conseille de placer le sujet aux deux tiers plutôt qu'au centre, pour obtenir une image mieux composée. On aura reconnu en 2/3 la première fraction réduite de l'inverse du nombre d'or: 2 et 3 sont deux nombre de Fibonacci consécutifs.
En peinture surtout, mais également en architecture, l'emploi du nombre d'or est tout à fait courant, sois sous forme de rectangle d'or, soit de l'un de ses dérivés.
L'art monumental des Égyptiens utilise largement la proportion dorée.
La grande pyramide de Khéops (IVème dynastie), est construite selon un triangle rectangle isocèle dont l'hypoténuse et le coté sont dans le rapport de PHI.
Par une coïncidence incroyable, un tel triangle est surnommé triangle égyptien. L'arête latérale de la pyramide mesure a*sqr(PHI^2+1), où 2a est le coté de la base.
On aura reconnu en a*sqr(PHI^2 + 1) la diagonale d'un pentagone inscrit dans un cercle.
Notons que l'on peut aussi trouver dans la même pyramide le nombre PI, et que ces propriétés se retrouvent dans d'autres pyramides (par exemple Mïdoum, IIIè dynastie).
On retrouve fréquemment le nombre d'or dans les dimensions des sarcophages, des tombeaux, et dans la statuaire - ce qui n'est surprenant, car dans corps humain, on retrouve souvent la proportion dorée (En particulier, si vous coupez un être humain en deux à hauteur du nombril - ce qui n'est pas à conseiller - vous obtiendrez deux parties dons le rapport est voisin du nombre d'or).
Plus proche de nous, le Parthénon est si riche en relation avec le nombre d'or qu'un ouvrage complet ne saurait épuiser le sujet.
Au moyen-âge, et surtout à la Renaissance, le nombre d'or était si indispensable aux bâtisseurs qu'ils avaient toujours dans leur trousse des abaques permettant de construire des triangles et des rectangles d'or.
certains de ces instruments sont visible au musée de Cluny à Paris.
Il suffit d'ouvrir le moindre ouvrage sur l'art gothique - ou mieux encore de visiter les cathédrales! - pour se rendre compte de l'importance de la présence du nombre d'or dans les canon de l'architecture gothique.
Encore plus proche de nous, Le Corbusier a imaginé et réalisé un système architectural basé sur le nombre d'or: le modulor.
En partant d'une dimension dimension de 175 cm, taille moyenne d'un humain, Le Corbusier construit une échelle de mesures se déduisant l'une de l'autre par le rapport de PHI.
Il semble d'ailleurs que l'harmonie universelle dont rêvait Le Corbusier n'ai pas été contagieuse, tant les critiques furent acerbes - et parfois injustifiées - envers ce poète du béton, qui pour beaucoup restera le créateur de la maison du fada.
En ce qui concerne la peinture, l'utilisation du nombre d'or - ici encore consciente ou inconsciente - est telle que l'on ne peut qu'inviter le lecteur à parcourir les musées armé d'un mètre-ruban et d'une calculatrice!
De Léonard de Vinci à Mondrian, en passant par David et surtout Ingres, tous ont flirté avec le nombre d'or.
S'il fallait étudier qu'un seul tableau, je retiendrais le Bain turc d'Ingres, tableau circulaire construit sur le pentagone étoilé inscrit.
Ou encore le fameux dessin de Léonard de Vinci représentant une homme (ne sachant pas encore qu'il posait pour une agence d'intérim) inscrit dans un pentagone régulier, ce qui vaut mieux que l'être au chômage.
On attend prochainement une thèse sur l'emploi du nombre d'or dans l'oeuvre graphique de Bruno Bellamy: La relation de Coussin et Confiture est-elle une relation dorée ?
Notons encore que le nombre d'or se retrouve dans des domaines où sa présence est plus étonnante encore: musique, littérature, etc.. mais ceci est une autre histoire.
Jean Pascal Duclos

Revenir au haut de la page